Solving Puzzles with Amb
Ever since an article about fibers, I was curious about an amb operator. There are multiple articles explaining both what it is and how to implement it: Roseta Code and Eric Kidd’s blog. There is even a gem with two different implementations. What’s left unclear to me, though was how to solve problems with amb.
I believe that the easiest way to understand something is to build it yourself and then try to explain it to others and that’s exactly what I’m doing now :)
Recently, I’ve solved a few classical problems using amb. The result turned out to be short, simple and declarative.
Disclaimer
The post turned out to be long, complex and code-heavy, but don’t let it discourage you. Please, try some of the things below. Play around it with it. They are mindblowing. A lisp ruby magic at it’s finest.
What exactly is amb and how it works
I really encourage you to read the articles I’ve mentioned above. You will better understand how it works under the hood. However, if you decide not to, here is a basic principle:
Given a set of constraints and options to choose from,
ambreturns options satisfied by those constraints.
And a basic example:
require 'amb'
x = amb(1, 2, 3, 4) # options to choose from
y = amb(1, 2, 3, 4) # options to choose from
amb unless x * y == 8 # constraint
puts "x: #{x}, y: #{y}"
=> x: 2, y: 4
Here we first specify options for x and y.Then we call amb without parameter until their product equals 8.
Why do we call amb without parameter? It’s a gem API to try other options by using a ruby control-flow structure called continuations. It allows as to easily check possible combinations until we find the one that satisfies the constraints.
Wait wait wait… What is a continuation?
I’ve mentioned them before, but without much explanation. The best way to describe continuations is through metaphor. If a program is a book, continuation would be a bookmark. Think of a goto, that can only go backward. Or using a famous sandwich example:
Say you’re in the kitchen in front of the refrigerator, thinking about a sandwich. You take a continuation right there and stick it in your pocket. Then you get some turkey and bread out of the refrigerator and make yourself a sandwich, which is now sitting on the counter. You invoke the continuation in your pocket, and you find yourself standing in front of the refrigerator again, thinking about a sandwich. But fortunately, there’s a sandwich on the counter, and all the materials used to make it are gone. So you eat it. :-)
Back to amb
Ok, so what amb gives us? Ability to specify a set of constraints and the ability to go backward in program execution and check different combinations of options until those constraints are met. Let’s see how it works in practice.
Note
- In all of the examples, I use gem amb.
- Examples don’t work in REPL, because irb/pry doesn’t handle continuations.
Problem 1: SEND + MORE = MONEY
Here is a classical cryptarithm. We need to change every single letter in the equation SEND + MORE = MONEY with a number such that it holds true.
The first naïve solution
The first thing I tried to do was just declaratively put requirements into code, like so
require 'amb'
include Amb::Operator
s = amb(1, 2, 3, 4, 5, 6, 7, 8, 9)
e = amb(1, 2, 3, 4, 5, 6, 7, 8, 9, 0)
n = amb(1, 2, 3, 4, 5, 6, 7, 8, 9, 0)
d = amb(1, 2, 3, 4, 5, 6, 7, 8, 9, 0)
m = amb(1, 2, 3, 4, 5, 6, 7, 8, 9)
o = amb(1, 2, 3, 4, 5, 6, 7, 8, 9, 0)
r = amb(1, 2, 3, 4, 5, 6, 7, 8, 9, 0)
y = amb(1, 2, 3, 4, 5, 6, 7, 8, 9, 0)
constraint = [s, e , n , d , m , o , r , y].uniq.size == 8 && "#{s}#{e}#{n}#{d}".to_i + "#{m}#{o}#{r}#{e}".to_i == "#{m}#{o}#{n}#{e}#{y}".to_i
amb unless constraint
As you can see, not very different from the basic example. Here we first specify options for every letter and then check that they are unique and equation holds true. Then we call amb without parameter until constraints are met.
It turned out to work but had a serious problem: speed. The code above took 13 minutes on my machine.
Optimized solution
Here is where Nikita Shilnikov came to the rescue. He showed, how to specify unique constraints when declaring amb options. This drastically reduced number of combinations we need to check
require 'amb'
include Amb::Operator
choices = (0..9).to_a
s = amb(*choices - [0])
e = amb(*choices - [s])
n = amb(*choices - [s, e])
d = amb(*choices - [s, e, n])
m = amb(*choices - [s, e, n, d, 0])
o = amb(*choices - [s, e, n, d, m])
r = amb(*choices - [s, e, n, d, m, o])
y = amb(*choices - [s, e, n, d, m, o, r])
constraint = "#{s}#{e}#{n}#{d}".to_i + "#{m}#{o}#{r}#{e}".to_i == "#{m}#{o}#{n}#{e}#{y}".to_i
amb unless constraint
puts "#{s}#{e}#{n}#{d} + #{m}#{o}#{r}#{e} = #{m}#{o}#{n}#{e}#{y}"
The example above takes a couple of seconds and it’s extremely elegant and declarative.
Problem 2: N-Queens Problem
The next problem we can solve with amb is harder and more interesting.
Description
Given the NxN chessboard, we need to place N queens such that they don’t threaten each other. Here’s a wiki if you want to know more.
Let’s think about how we can solve it using amb.
Notes on implementation
- We need to specify the row and the column of the queen. We can use a simple array for that.
- Rows and columns are unique.
- We need some simple way to check if two queens are on the same diagonal. Quick StackOverflow search suggests that we should check the slope between two queens and if it’s the same, they are on the same diagonal, like so:
(queen1X - queen2X).abs == (quuen1Y - queen2Y).abs
That’s enough for us to put together a solution
Implementation
First, we specify the number of queens and create them
n = 8
queens = Array.new(n) { [0, 0] }
We need a unique row, column and diagonal. We could use amb for both row and column, but the result will be super slow and a unique diagonal can be found just by changing column. That’s why we hardcode a row and use amb only for a column.
choices = [*1..n]
n.times do |i|
column = amb(*choices - queens[0..i].map(&:first))
row = i + 1
queens[i] = [column, row]
end
We check diagonals using the formula for checking slopes
different_diags = queens.each.with_index.all? do |q1, i|
(queens[i..-1] - [q1]).none? do |q2|
(q1.first - q2.first).abs == (q1.last - q2.last).abs
end
end
And try again until the constraint is met
amb unless different_diags
Full solution
require 'amb'
include Amb::Operator
n = 8
queens = Array.new(n) { [0, 0] }
choices = [*1..n]
n.times do |i|
column = amb(*choices - queens[0..i].map(&:first))
row = i + 1
queens[i] = [column, row]
end
different_diags = queens.each.with_index.all? do |q1, i|
(queens[i..-1] - [q1]).none? do |q2|
(q1.first - q2.first).abs == (q1.last - q2.last).abs
end
end
amb unless different_diags
puts queens.inspect
Again, a declarative solution is a few lines long compared to a procedural one
Problem 3: 4 Color problem
In our last problem, we’ll try to color a map of Europe, using only 4 colors such that no neighborhood countries had the same color.
With amb, the solution is rather straightforward.
Implementation
We specify possible colors and countries
require 'amb'
include Amb::Operator
choices = %i(green yellow red blue)
countries = {
portugal: { neighbors: %i(spain), color: nil },
spain: { neighbors: %i(portugal andorra france), color: nil },
andorra: { neighbors: %i(spain france), color: nil },
france: { neighbors: %i(spain andorra monaco italy switzerland germany luxembourg belgium united_kingdom), color: nil },
united_kingdom: { neighbors: %i(france belgium netherlands denmark norway iceland ireland), color: nil },
ireland: { neighbors: %i(united_kingdom iceland), color: nil },
monaco: { neighbors: %i(france), color: nil },
italy: { neighbors: %i(france greece albania montenegro croatia slovenia austria switzerland san_marino), color: nil },
san_marino: { neighbors: %i(italy), color: nil },
switzerland: { neighbors: %i(france italy austria germany liechtenstein), color: nil },
liechtenstein: { neighbors: %i(switzerland austria), color: nil },
germany: { neighbors: %i(france switzerland austria czech_republic poland sweden denmark netherlands belgium luxembourg), color: nil },
belgium: { neighbors: %i(france luxembourg germany netherlands), color: nil },
netherlands: { neighbors: %i(belgium germany united_kingdom), color: nil },
luxembourg: { neighbors: %i(france germany belgium), color: nil },
austria: { neighbors: %i(italy slovenia hungary slovakia czech_republic germany switzerland liechtenstein), color: nil },
slovenia: { neighbors: %i(italy croatia hungary austria), color: nil },
croatia: { neighbors: %i(italy montenegro bosnia serbia hungary slovenia), color: nil },
bosnia: { neighbors: %i(croatia montenegro serbia), color: nil },
montenegro: { neighbors: %i(croatia italy albania serbia bosnia), color: nil },
albania: { neighbors: %i(italy greece macedonia serbia montenegro), color: nil },
greece: { neighbors: %i(italy cyprus bulgaria macedonia albania), color: nil },
cyprus: { neighbors: %i(greece), color: nil },
macedonia: { neighbors: %i(albania greece bulgaria serbia), color: nil },
bulgaria: { neighbors: %i(macedonia greece romania serbia), color: nil },
serbia: { neighbors: %i(montenegro albania macedonia bulgaria romania hungary croatia bosnia), color: nil },
romania: { neighbors: %i(serbia bulgaria hungary moldova), color: nil },
hungary: { neighbors: %i(slovenia croatia serbia romania slovakia austria ukraine), color: nil },
slovakia: { neighbors: %i(austria hungary poland czech_republic ukraine), color: nil },
czech_republic: { neighbors: %i(germany austria slovakia poland), color: nil },
poland: { neighbors: %i(germany czech_republic slovakia sweden ukraine lithuania belarus), color: nil },
denmark: { neighbors: %i(united_kingdom germany sweden norway), color: nil },
sweden: { neighbors: %i(norway denmark germany poland finland), color: nil },
norway: { neighbors: %i(united_kingdom denmark sweden finland iceland), color: nil },
finland: { neighbors: %i(sweden norway), color: nil },
iceland: { neighbors: %i(ireland united_kingdom norway), color: nil },
ukraine: { neighbors: %i(slovakia moldova poland belarus hungary), color: nil },
moldova: { neighbors: %i(ukraine romania), color: nil },
belarus: { neighbors: %i(poland ukraine lithuania latvia), color: nil },
lithuania: { neighbors: %i(poland belarus latvia), color: nil },
estonia: { neighbors: %i(latvia), color: nil },
latvia: { neighbors: %i(estonia belarus lithuania), color: nil },
}
Specify their possible color
countries.each do |country, value|
neighborhood_country_colors = countries
.values_at(*value[:neighbors])
.map { |c| c[:color] }.compact.uniq
countries[country][:color] = amb(*choices - neighborhood_country_colors)
end
Check that they are different
different_colors = countries.none? do |country, value|
countries.values_at(*value[:neighbors])
.map { |c| c[:color] }
.include?(value[:color])
end
Try until the constraint is true
ruby
amb unless different_colors
Full solution
require 'amb'
include Amb::Operator
choices = %i(green yellow red blue)
countries = {
portugal: { neighbors: %i(spain), color: nil },
spain: { neighbors: %i(portugal andorra france), color: nil },
andorra: { neighbors: %i(spain france), color: nil },
france: { neighbors: %i(spain andorra monaco italy switzerland germany luxembourg belgium united_kingdom), color: nil },
united_kingdom: { neighbors: %i(france belgium netherlands denmark norway iceland ireland), color: nil },
ireland: { neighbors: %i(united_kingdom iceland), color: nil },
monaco: { neighbors: %i(france), color: nil },
italy: { neighbors: %i(france greece albania montenegro croatia slovenia austria switzerland san_marino), color: nil },
san_marino: { neighbors: %i(italy), color: nil },
switzerland: { neighbors: %i(france italy austria germany liechtenstein), color: nil },
liechtenstein: { neighbors: %i(switzerland austria), color: nil },
germany: { neighbors: %i(france switzerland austria czech_republic poland sweden denmark netherlands belgium luxembourg), color: nil },
belgium: { neighbors: %i(france luxembourg germany netherlands), color: nil },
netherlands: { neighbors: %i(belgium germany united_kingdom), color: nil },
luxembourg: { neighbors: %i(france germany belgium), color: nil },
austria: { neighbors: %i(italy slovenia hungary slovakia czech_republic germany switzerland liechtenstein), color: nil },
slovenia: { neighbors: %i(italy croatia hungary austria), color: nil },
croatia: { neighbors: %i(italy montenegro bosnia serbia hungary slovenia), color: nil },
bosnia: { neighbors: %i(croatia montenegro serbia), color: nil },
montenegro: { neighbors: %i(croatia italy albania serbia bosnia), color: nil },
albania: { neighbors: %i(italy greece macedonia serbia montenegro), color: nil },
greece: { neighbors: %i(italy cyprus bulgaria macedonia albania), color: nil },
cyprus: { neighbors: %i(greece), color: nil },
macedonia: { neighbors: %i(albania greece bulgaria serbia), color: nil },
bulgaria: { neighbors: %i(macedonia greece romania serbia), color: nil },
serbia: { neighbors: %i(montenegro albania macedonia bulgaria romania hungary croatia bosnia), color: nil },
romania: { neighbors: %i(serbia bulgaria hungary moldova), color: nil },
hungary: { neighbors: %i(slovenia croatia serbia romania slovakia austria ukraine), color: nil },
slovakia: { neighbors: %i(austria hungary poland czech_republic ukraine), color: nil },
czech_republic: { neighbors: %i(germany austria slovakia poland), color: nil },
poland: { neighbors: %i(germany czech_republic slovakia sweden ukraine lithuania belarus), color: nil },
denmark: { neighbors: %i(united_kingdom germany sweden norway), color: nil },
sweden: { neighbors: %i(norway denmark germany poland finland), color: nil },
norway: { neighbors: %i(united_kingdom denmark sweden finland iceland), color: nil },
finland: { neighbors: %i(sweden norway), color: nil },
iceland: { neighbors: %i(ireland united_kingdom norway), color: nil },
ukraine: { neighbors: %i(slovakia moldova poland belarus hungary), color: nil },
moldova: { neighbors: %i(ukraine romania), color: nil },
belarus: { neighbors: %i(poland ukraine lithuania latvia), color: nil },
lithuania: { neighbors: %i(poland belarus latvia), color: nil },
estonia: { neighbors: %i(latvia), color: nil },
latvia: { neighbors: %i(estonia belarus lithuania), color: nil },
}
countries.each do |country, value|
neighborhood_country_colors = countries.values_at(*value[:neighbors])
.map { |c| c[:color] }
.compact
.uniq
countries[country][:color] = amb(*choices - neighborhood_country_colors)
end
different_colors = countries.none? do |country, value|
countries.values_at(*value[:neighbors])
.map { |c| c[:color] }
.include?(value[:color])
end
amb unless different_colors
countries.each { |c, v| puts "#{c}: #{v[:color]}" }
Result
Here is what we get if we run the code
portugal: green
spain: yellow
andorra: green
france: red
united_kingdom: green
ireland: yellow
monaco: green
italy: green
san_marino: yellow
switzerland: yellow
liechtenstein: green
germany: green
belgium: yellow
netherlands: red
luxembourg: blue
austria: red
slovenia: yellow
croatia: red
bosnia: green
montenegro: yellow
albania: red
greece: yellow
cyprus: green
macedonia: green
bulgaria: red
serbia: blue
romania: yellow
hungary: green
slovakia: yellow
czech_republic: blue
poland: red
denmark: yellow
sweden: blue
norway: red
finland: green
iceland: blue
ukraine: blue
moldova: green
belarus: green
lithuania: yellow
estonia: green
latvia: red
I wasn’t sure that the code worked correctly so I’ve decided to color the map with the colors above. Here is the result
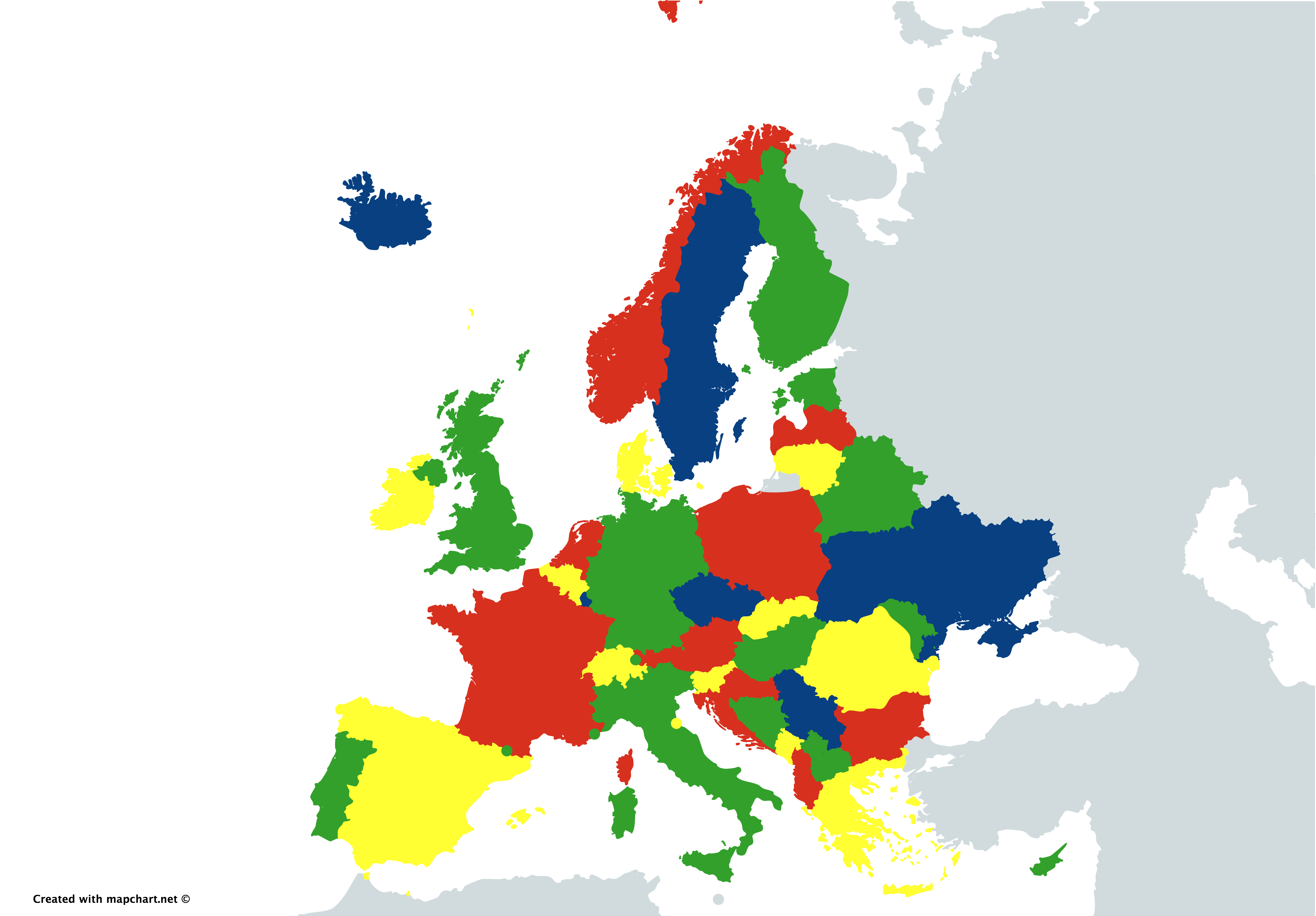
As you can see, all neighborhood countries have different colors.
Thanks for reading!
Amb and the puzzles don’t really have any pragmatic value, but I feel that in programming there is always room for things that are just fun and magical. Hope you’ve enjoyed reading the post.
